formulación de modelos

                                     FORMULACIÓN DE MODELOS

TIPOS DE MODELOS:

(a) Modelo Matemático: Se emplea cuando la función objetivo y las restricciones del modelo se pueden expresar en forma cuantitativa o matemática como funciones de las variables de decisión.

(b) Modelo de Simulación: Los modelos de simulación difieren de los matemáticos en que las relación entre la entrada y la salida no se indican en forma explícita. En cambio, un modelo de simulación divide el sistema representado en módulos básicos o elementales que después se enlazan entre si vía relaciones lógicas bien definidas. Por lo tanto, las operaciones de cálculos pasaran de un módulo a otro hasta que se obtenga un resultado de salida.

Los modelos de simulación cuando se comparan con modelos matemáticos; ofrecen mayor flexibilidad al representar sistemas complejos, pero esta flexibilidad no esta libre de inconvenientes. La elaboración de este modelo suele ser costoso en tiempo y recursos. Por otra parte, los modelos matemáticos óptimos suelen poder manejarse en términos de cálculos.

Modelos de Investigación de Operaciones de la ciencia de la administración: Los científicos de la administración trabajan con modelos cuantitativos de decisiones.

Modelos Formales: Se usan para resolver problemas cuantitativos de decisión en el mundo real. Algunos modelos en la ciencia de la administración son llamados modelos deterministicos. Esto significa que todos los datos relevantes (es decir, los datos que los modelos utilizarán o evaluarán) se dan por conocidos. En los modelos probabilísticos (o estocásticos), alguno de los datos importantes se consideran inciertos, aunque debe especificarse la probabilidad de tales datos.

En la siguiente tabla se muestran los modelos de decisión según su clase de incertidumbre y su uso en las corporaciones. (D, determinista; P, probabilista; A, alto; B, bajo)

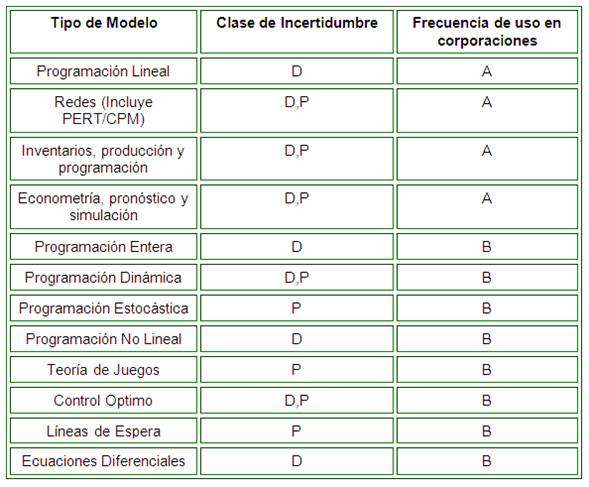
Modelo de Hoja de Cálculo Electrónica: La hoja de cálculo electrónica facilita hacer y contestar preguntas de "que si" en un problema real. Hasta ese grado la hoja de cálculo electrónica tiene una representación selectiva del problema y desde este punto de vista la hoja de cálculo electrónica es un modelo.

En realidad es una herramienta más que un procedimiento de solución. 

Etapas de la Investigación de Operaciones 

Las etapas de un estudio de Investigación de Operaciones son las siguientes:

Definición del problema de interés y recolección de los datos relevantes.

Formulación de un modelo matemático que represente el problema.

Desarrollo de un procedimiento basado en computadora para derivar una solución al problema a partir del modelo.

Prueba del modelo y mejoramiento según sea necesario.

Preparación para la aplicación del modelo prescrito por la administración.

Puesta en marcha. 

El método Simplex es un procedimiento interactivo que permite ir mejorando la solución a cada paso. El proceso concluye cuando no es posible seguir mejorando más dicha solución.

Partiendo del valor de la función objetivo en un vértice cualquiera, el método consiste en buscar sucesivamente otro vértice que mejore al anterior. La búsqueda se hace siempre a través de los lados del polígono (o de las aristas del poliedro, si el número de variables es mayor). Cómo el número de vértices (y de aristas) es finito, siempre se podrá encontrar la solución.

El método Simplex se basa en la siguiente propiedad: si la función objetivo, f, no toma su valor máximo en el vértice A, entonces hay una arista que parte de A, a lo largo de la cual f aumenta.

Deberá tenerse en cuenta que este método sólo trabaja para restricciones que tengan un tipo de desigualdad "=" y coeficientes independientes mayores o iguales a 0, y habrá que estandarizar las mismas para el algoritmo. En caso de que después de éste proceso, aparezcan (o no varíen) restricciones del tipo "=" o "=" habrá que emplear otros métodos, siendo el más común el método de las Dos Fases.

DESARROLLANDO EL MÉTODO SIMPLEX

Una vez que hemos estandarizado nuestro modelo, puede ocurrir que necesitemos aplicar el método Simplex o el método de las Dos Fases. Véase en la figura como debemos actuar para llegar a la solución de nuestro problema.

El método del simplex fue creado en 1947 por el matemático George Dantzig .

El método del simplex se utiliza, sobre todo, para resolver problemas de programación lineal en los que intervienen tres o más variables.

El álgebra matricial y el proceso de eliminación de Gauss-Jordan para resolver un sistema de ecuaciones lineales constituyen la base del método simplex.

Es un procedimiento iterativo que permite ir mejorando la solución a cada paso. El proceso concluye cuando no es posible seguir mejorando más dicha solución.

Partiendo del valor de la función objetivo en un vértice cualquiera, el método consiste en buscar sucesivamente otro vértice que mejore al anterior. La búsqueda se hace siempre a través de los lados del polígono (o de las aristas del poliedro, si el número de variables es mayor). Cómo el número de vértices (y de aristas) es finito, siempre se podrá encontrar la solución.

El método del simplex se basa en la siguiente propiedad: si la función objetivo, f, no toma su valor máximo en el vértice A, entonces hay una arista que parte de A, a lo largo de la cual f aumenta.

Con miras a conocer la metodología que se aplica en el Método SIMPLEX, vamos a resolver el siguiente problema:

Se consideran las siguientes fases:

1. Convertir las desigualdades en igualdades

Se introduce una variable de holgura por cada una de las restricciones, para convertirlas en igualdades, resultando el sistema de ecuaciones lineales:

2. Igualar la función objetivo a cero

- 3x - 2y + Z = 0

3. Escribir la tabla inicial simplex

En las columnas aparecerán todas las variables del problema y, en las filas, los coeficientes de las igualdades obtenidas, una fila para cada restricción y la última fila con los coeficientes de la función objetivo:

SOLUCIÓN BÁSICA INICIAL FACTIBLE – S.B.I.F.

1. Se obtiene una Solución Básica Inicial por medio de la Forma Estándar del modelo, es decir, convertir las desigualdades en igualdades introduciendo variables de holgura (=).

Una Solución Básica es una Solución Básica Factible sí y sólo sí las variables Básicas tienen valores no negativos, es decir, mayores o iguales a cero (>=).

2. Debe existir en cada ecuación una variable con coeficiente +1 y que no este en ninguna otra restricción; las otras variables con coeficiente cero (0) para formar el Canónico o Base del sistema de ecuaciones. Se obtiene una Solución Básica Factible Inicial inicializando n-m variables adecuadas (No Básicas) al nivel de cero.

Donde: n Número de incógnitas

m Número de restricciones o ecuaciones

m < n

La función Objetivo no se tiene en cuenta para determinar el sistema de ecuaciones, aunque hace parte del Canónico.

Clasificación de modelos 

Los modelos se clasifican desde diversos puntos de vista. Es de advertir que las siguientes divisiones y subdivisiones no fueron realizadas en forma exhaustiva. 

1.1    Por su grado de abstracción: 

se dividen en abstractos (no físicos) y concretos (físicos). Los primeros en general se apartan de la realidad y los segundos generalmente emulan los sistemas reales Los modelos lineales trabajan con funciones lineales en tanto que los modelos no lineales utilizan funciones no lineales.

1.2Por su esencia:

son normativos y descriptivos. Los modelos primeros indican normas que se deben cumplir, mientras que los segundos nos definen una situación real.

1.3Por sus características:

 pueden ser réplicas, cuasirréplicas, analógicos, formalización, isomorfos y simulación. Réplica, representación estricta de la realidad a escala; cuasirréplica, su representación se realiza en dos dimensiones; analógicos, utilizan unas propiedades para representar otras; formalización, emplean lenguaje abstracto; isomorfos, número de variables que emplea el modelo; simulación, no se reproducen características físicas